Pruning the Sudoku Tree
Sudokus: everybody knows them, many have love-hate relationships with them, and one can find them literally everywhere, from newspapers to kiosks. Sudokus are great way to idle away time, and exercise the nogging.
They are also incredibly boring. So let's solve them programmatically.
The rules of sudoku is simple: we have a 9x9 grid, with some numbers already filled in. The goal is to fill in the rest of the grid with numbers from 1 to 9, such that every row, column, and outlined box has no duplicate numbers.
So, how can we solve it? Easy! We just have to fill in all of the squares with a number, check if its a valid solution, and if not, try another. We'll take as input a one-dimensional array representing the sudoku grid (the reason I didn't use a 2D array is, quite frankly, laziness), and modify the sudoku grid in place. The entries in the array are either the numbers 1 to 9 as strings, or a period (.) to represent an empty square. We'll return True if a solution has been found, and False otherwise. Here's the code in Python:
def naive_solve(sudoku):
try:
i = sudoku.index('.')
except ValueError:
#The grid is full, so we check if we have a valid grid.
return is_valid(sudoku)
for n in range(1,10):
sudoku[i] = str(n)
if (naive_solve(sudoku)):
return True
sudoku[i] = '.'
return False
There we go, super sim...

...oh, that's going to take forever. We need a better solution.
Get The Shears, We're Pruning!
So, why's the article titled so? Whenever you are refining a searching algorithm's area of search, you are doing a process known as pruning.

To elaborate further, we can imagine the process of solving a sudoku in the form of a tree. Each node represents a partially filled in sudoku grid, and each edge represents filling a particular square with a particular number.
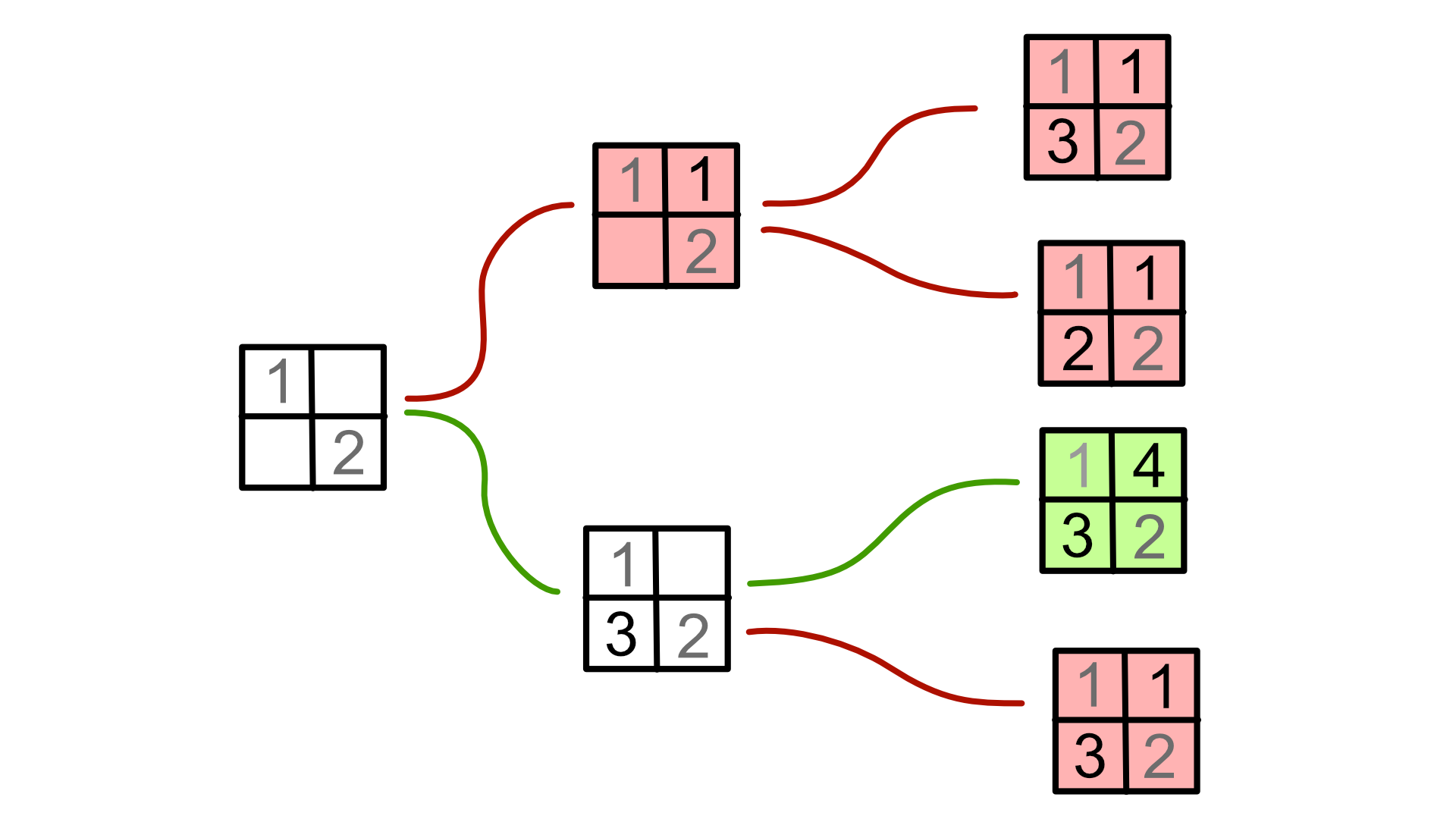
Now, most of these branches are dead ends. These represents the cases where we've made a mistake when trying to solve the sudoku. Some branches, however, leads to the correct solution. The goal, then, is to find a 'path' of sorts that leads us to that correct solution.
One way to try to find said path is by brute force: try every path until you've found the correct one. That is essentially what naive_solve is. Of course, if the tree is sufficiently large, this can take forever. So, to help reduce search time, we should focus on reducing the size of the tree, by effectively 'pruning' off the branches that certainly lead nowhere.
One easy fix to our algorithm: instead of checking if our grid is valid once all the numbers are filled in, we could instead check as we fill in the squares. That way, if we introduce an error early, we can save ourselves the trouble of calculating a bunch of obviously wrong grids:
def backtrack_solve(sudoku):
try:
i = sudoku.index('.')
except ValueError:
return True
for n in range(1,10):
sudoku[i] = str(n)
#validate index just performs validation at index i instead of the whole grid
if (validate_index(sudoku, i) and backtrack_solve(sudoku)):
return True
sudoku[i] = '.'
return False
As an aside, the reason this algorithm is called backtrack_solve is simply because that is what this strategy is: from some partially filled sudoku grid, we pick a square, try every possibility, and if it doesn't work, this means we made an error previously, and so we must backtrack to try something else.
Already, this runs much better. However, this algorithm is still not feasible for 17-clue puzzles, which is the holy grail of sudoku puzzles. We need more.

Ordering Matters
Imagine you are doing a sudoku, and you've run out of obvious squares to fill. It's time to make a guess. Which square would you chose? Most people's answer would be "the square with the least possibilities", since you have the highest likelihood of guessing the right answer, and on the off chance you are wrong, eliminating one option out of a small handful of options is more impactful than out of a large amount. In terms of our search tree, we chose the options with the fewest branches early on, since that is when decisions are most impactful.
To keep track of this data, we'll keep an array of size 9 for each square, which we call poslist. The entry poslist[s][i] is either a period (.) if placing the value i+1 in square s would still keep the sudoku valid, or the index of the square that prevents the value of i+1 to be placed in this square. For example, on an empty grid, the array of square 0 (which would be the top left square) is entirely periods. If we then place the number 1 in the top right square (with index 8), we would now have poslist[0][0] = 8. The updating process looks like so:
def prune(index, val, poslist):
indval = val-1
row = index // 9
col = index % 9
box_row = row // 3
box_col = col // 3
for i in range(9):
checkedindex = row*9 + i
if poslist[checkedindex][indval] == '.':
poslist[checkedindex][indval] = index
for j in range(9):
checkedindex = col + j*9
if poslist[checkedindex][indval] == '.':
poslist[checkedindex][indval] = index
for i in range(3):
for j in range(3):
checkedindex = (box_row*3 + i)*9 + (box_col*3 + j)
if poslist[checkedindex][indval] == '.':
poslist[checkedindex][indval] = index
Perhaps you might be asking why use something this complex. The main reason is so that we can easily reverse this process, like so:
def unprune(index, val, poslist):
indval = val-1
row = index // 9
col = index % 9
box_row = row // 3
box_col = col // 3
for i in range(9):
checkedindex = row*9 + i
if poslist[checkedindex][indval] == index:
poslist[checkedindex][indval] = '.'
for j in range(9):
checkedindex = col + j*9
if poslist[checkedindex][indval] == index:
poslist[checkedindex][indval] = '.'
for i in range(3):
for j in range(3):
checkedindex = (box_row*3 + i)*9 + (box_col*3 + j)
if poslist[checkedindex][indval] == index:
poslist[checkedindex][indval] = '.'
This makes backtracking much easier.
So, the code:
def least_possibilities_solve(sudoku, poslist):
mincount = 10
mincountindex = -1
#Finds the best possible square to evaluate.
for i in range(len(sudoku)):
if sudoku[i] == '.':
count = poslist[i].count('.')
#If count == 0 then there is an empty square that
# doesn't have any values.
if (count == 0):
return False
if (mincount > count):
mincount = count
mincountindex = i
#mincountindex == -1 means the grid is full.
if (mincountindex == -1):
return True
for n in range(1,10):
if (poslist[mincountindex][n-1] == '.'):
sudoku[mincountindex] = str(n)
prune(mincountindex,n,poslist)
if (least_possibilities_solve(sudoku, poslist)):
return True
unprune(mincountindex,n,poslist)
sudoku[mincountindex] = '.'
return False
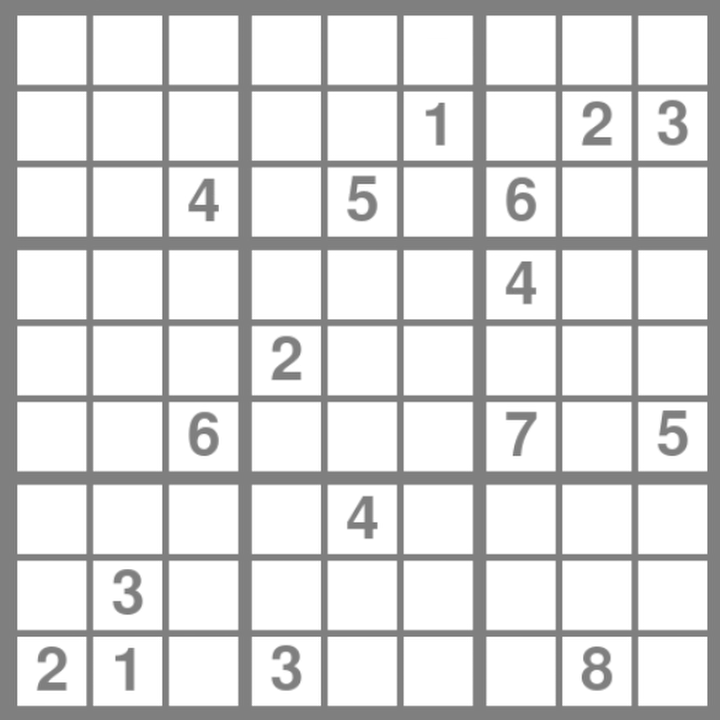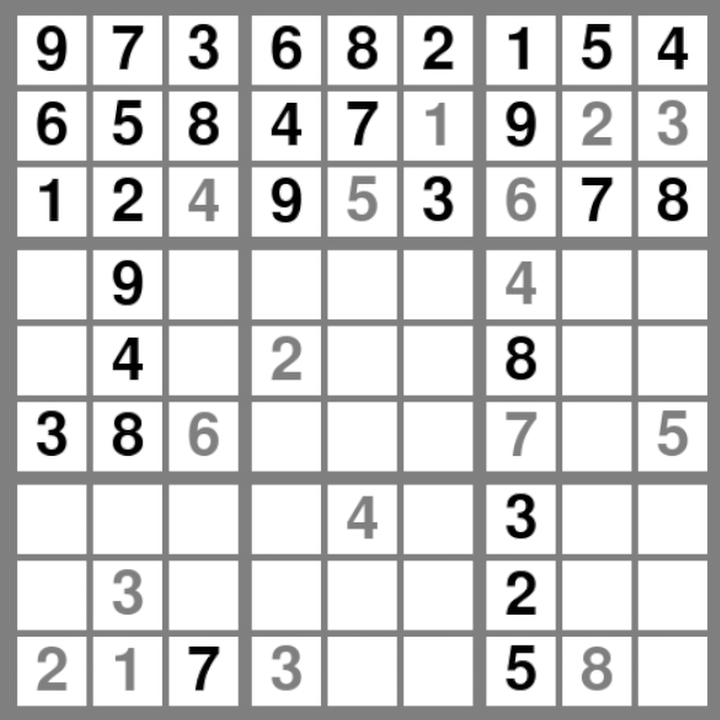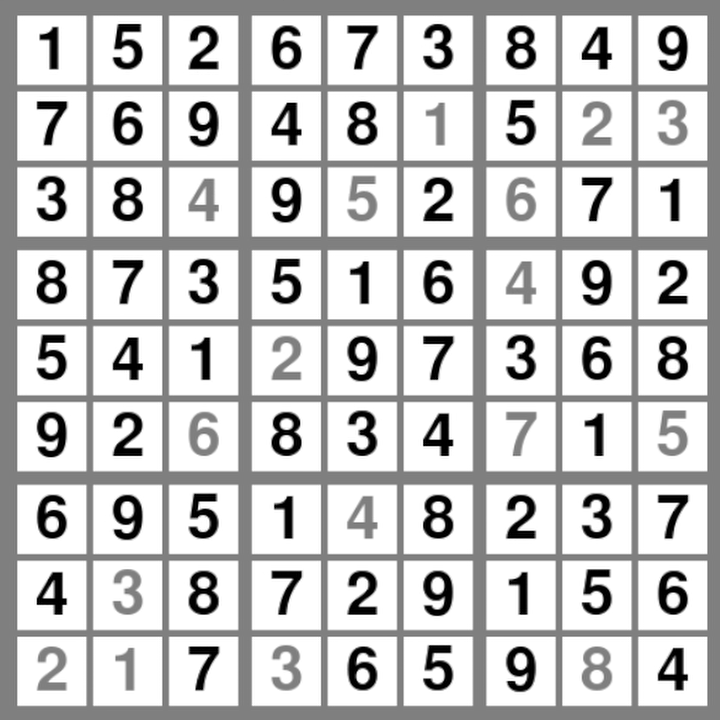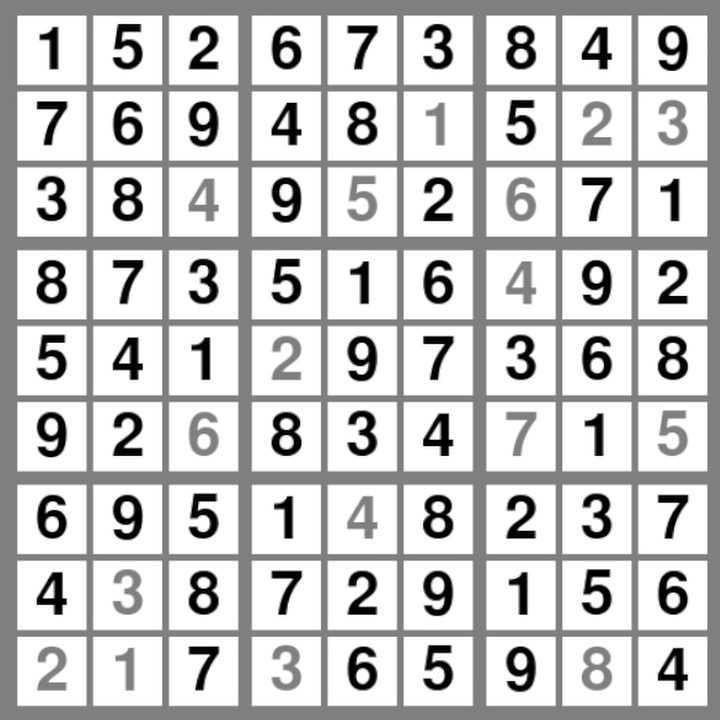
This code runs much better that backtrack_solve, but it still takes a second to compute, and that's simply too long. We can do better!
Don't Forget the Basics
Probably why this algorithm is struggling so much is because we haven't even implemented the most basic strategy. Look at the grid below.
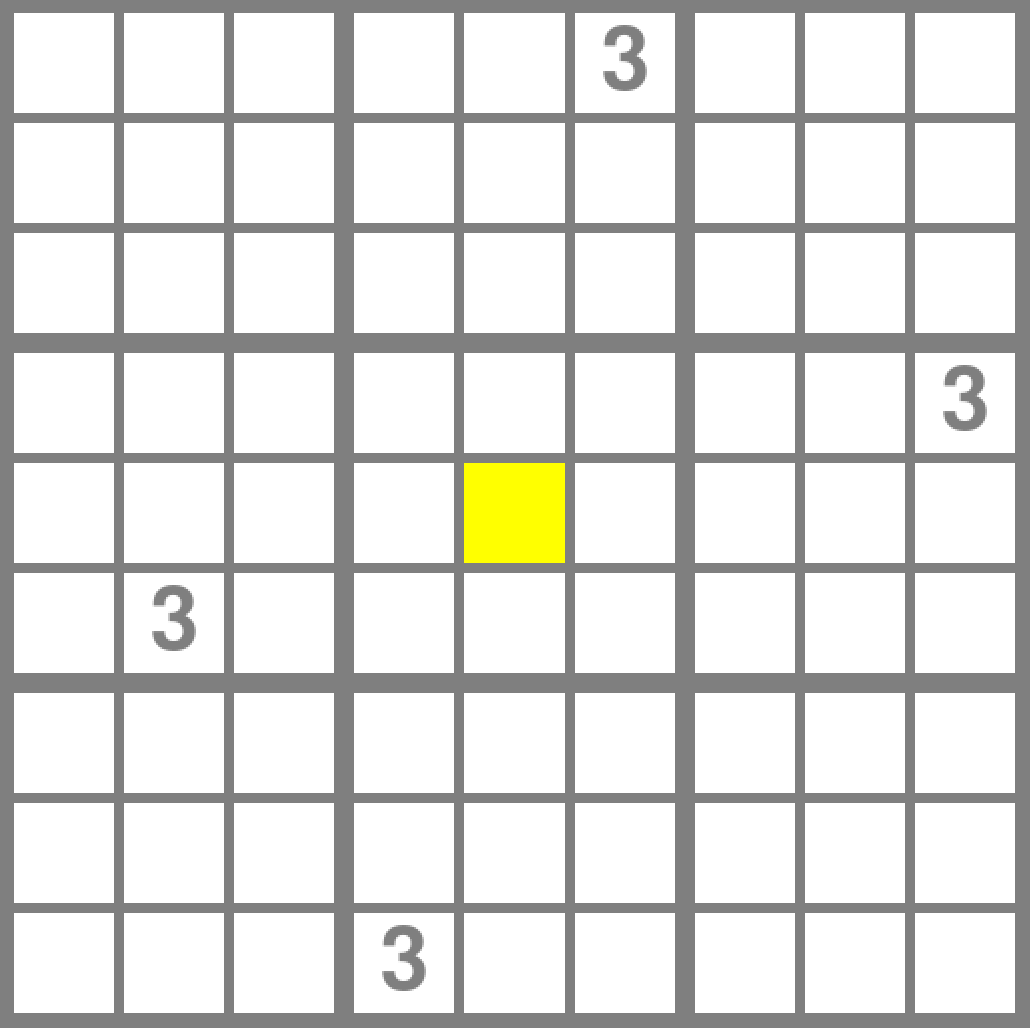
Hopefully, if you're familiar enough with sudokus, you should have realised that there is only one place to put a 3 in the centre box. Since we're forced to put a 3 in one spot, might as well put it there!
We'll keep track of this data with a bunch of sets, which we'll store in poslistcount. Specifically, for each row, column, and box, we'll keep 9 sets, one for each number 1 to 9. Each set will store the indexes of squares in their respective area, that can accept the set's number without conflict. For example, in the following diagram, the set for the number 1 in row 1 contains the numbers 0,1,2,3 and 5.
Then, if any of the sets winds up being a singleton (a set with one element), this tells us that we are forced to place a specific value at the index in the set.
We'll use two helper functions for this. The first one updates poslistcount appropriately:
#Update poslist at the relevant index. change tells us whether or not we are allowed
# to place val at index: if change = 1, then we are allowed, if change=-1, then we are
# not allowed.
def update_poslistcount(index, poslistcount, val, change):
if (change == 1):
poslistcount[0][index // 9][val].add(index)
poslistcount[1][index % 9][val].add(index)
poslistcount[2][(index // 27)*3 + (index % 9)//3][val].add(index)
elif (change == -1):
poslistcount[0][index // 9][val].discard(index)
poslistcount[1][index % 9][val].discard(index)
poslistcount[2][(index // 27)*3 + (index % 9)//3][val].discard(index)
The second helper is for finding singleton sets:
#Finds a singleton set in poslistcount, returns the index and associated value
def find_forced(poslistcount):
for i in range(len(poslistcount)):
for j in range(len(poslistcount[i])):
for k in range(len(poslistcount[i][j])):
if (len(poslistcount[i][j][k]) == 1):
for e in poslistcount[i][j][k]:
return e, k+1
return -1, -1
We'll then need to update prune in order to update poslistcount appropriately:
def count_prune(index, val, poslist, poslistcount):
#Previously we didn't need to update poslist for squares
# with a number filled in, since we never used that information.
# However, in order to update poslistcount properly, we need
# to keep track of this information now.
for i in range(9):
if poslist[index][i] == '.':
poslist[index][i] = index
update_poslistcount(index, poslistcount, i, -1)
indval = val-1
row = index // 9
col = index % 9
box_row = row // 3
box_col = col // 3
for i in range(9):
checkedindex = row*9 + i
if poslist[checkedindex][indval] == '.':
poslist[checkedindex][indval] = index
update_poslistcount(checkedindex, poslistcount, indval, -1)
for j in range(9):
checkedindex = col + j*9
if poslist[checkedindex][indval] == '.':
poslist[checkedindex][indval] = index
update_poslistcount(checkedindex, poslistcount, indval, -1)
for i in range(3):
for j in range(3):
checkedindex = (box_row*3 + i)*9 + (box_col*3 + j)
if poslist[checkedindex][indval] == '.':
poslist[checkedindex][indval] = index
update_poslistcount(checkedindex, poslistcount, indval, -1)
unprune is similarly modified. Finally, we have the actual algorithm:
#poslistcount keeps track of the number of square in a row/column/box that
# can have a certain value. When a certain entry is 1, this tells us that
# some row/col/box has only one square in which a value can exist, a.k.a.
# we are forced to put a value in a position
def with_force_solve(sudoku, poslist, poslistcount):
mincount = 10
mincountindex = -1
#Finds the best possible square to evaluate.
forcedindex, forcedval = find_forced(poslistcount)
if forcedindex != -1:
mincountindex = forcedindex
else:
for i in range(len(sudoku)):
if sudoku[i] == '.':
count = poslist[i].count('.')
#If count == 0 then there is an empty square that
# doesn't have any values.
if (count == 0):
return False
if (mincount > count):
mincount = count
mincountindex = i
#mincountindex == -1 means the grid is full.
if (mincountindex == -1):
return True
for n in range(1,10):
if (forcedindex == -1 and poslist[mincountindex][n-1] == '.') or forcedval == n:
sudoku[mincountindex] = str(n)
count_prune(mincountindex,n,poslist, poslistcount)
if (with_force_solve(sudoku, poslist, poslistcount)):
return True
count_unprune(mincountindex,n,poslist, poslistcount)
sudoku[mincountindex] = '.'
return False
And there we have it! Let's test it out.
As you can see, near instant on 17-clue sudokus. In fact, this algorithm can solve hundreds per second. In fact, this algorithm is capable of solving 49,158 17-clue sudokus in under 3 minutes!

Final Thoughts
I could probably go further and try to implement more complicated algorithms, but I doubt it'll be worth the effort. The more complicated we make our algorithm, the greater the overhead becomes in terms of memory usage and execution time. Furthermore, our final strategy is already pretty good: for a lot of sudokus, the search tree becomes a single line!
If you want to play around with these algorithms, I have put them in a GitHub repo, with a handy gui for easy interaction. You can find them here. Note that this program doesn't come with the sudoku puzzles; you'll have to download them yourself. For this article, I used the data from t-dillon which you can find here.
