On The Topic of 0.999... = 1
So, the topic-du-jour in the maths reddit communities is one that comes up from time to time. It's this:
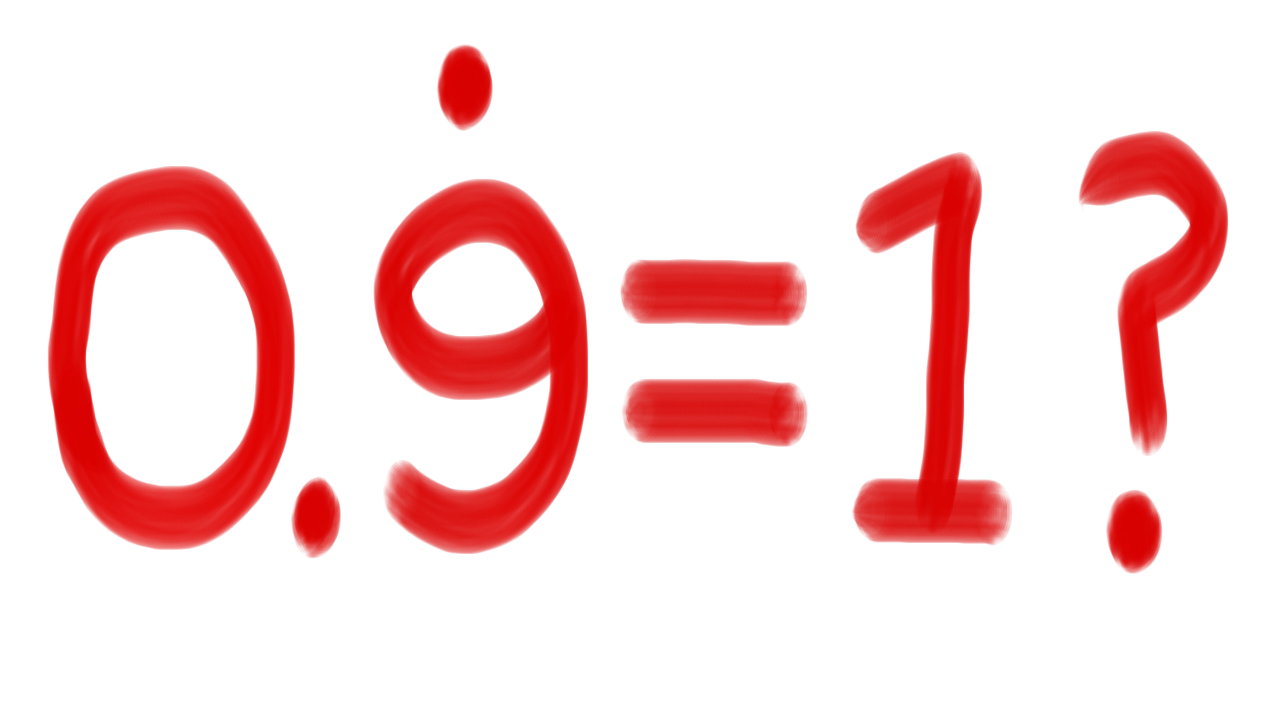
In fairness, if you've not seen this before, the result might seem counter-intuitive. After all, we're generally taught that numbers with different decimals are distinct. But, as many generations of mathematicians have figured out, the above statement is true in the real numbers. While this article isn't strictly about the real numbers, I'll underline two different proofs (for use later).
Proof 1 - Epsilon
The first proof directly uses the definition of a decimal. Namely, \(0.999\dots\) is defined to be equal to the series \[\sum_{i=1}^{\infty} 9 \frac{1}{10^i}.\] Since this is an infinite series, we use the epsilon definition of limits to show that \(0.999\dots\) does indeed equal \(1\).
Let \(\epsilon > 0\). There exists \(k \in \mathbb{N}\) such that \(\frac{1}{10^k} < \epsilon\). Then, for all \(m > k\), we get \(\left|1-\sum_{i=1}^{m} 9 \frac{1}{10^i}\right| = \frac{1}{10^m} < \frac{1}{10^k} < \epsilon\), which satisfies the epsilon definition of a limit. Therefore, \(0.999\dots = 1\).
Technically, this proof use a hidden assumption. Namely, it's that for any positive value of \(\epsilon\) that we choose, we can find a positive integer \(k\) with \(\frac{1}{10^k} < \epsilon\). This property is known as the archimedean property, and I'll talk more about this later.
Proof 2 - Algebra
The other proof is more algebraic in nature, but it is much easier to understand.
Let \(x = 0.999\dots\). Then,
\begin{align*} x &= 0.999\dots &\\ 10x &= 9.999\dots&\\ 9x &= 9 &\text{ (By subtracting line 1 from line 2)}\\ x &= 1.& \end{align*}
Thus \(0.999\dots = 1\).
This proof uses a different property, namely that of the algebra of limits. Roughly, this property means that we can add and multiply sequence together, and the limit of the resulting sequences is equal to the limits of the original sequences added or multiplied together (depending on how the sequences were combined). The benefit of this method of proof is that the algebra of limits applies generally to any field, not just the real numbers.
Alright, so there are our two proofs. Now, on to the actual subject of this article.
Hyperreals, what are they?
I think the first time I encountered the notion of hyperreal numbers was in this exact context: a way of making \(0.999\dots \neq 1\). Which is why, when this topic rolled around again, I though it a good opportunity to actually plunge into this particular rabbit hole.
So, what are the hyperreal numbers? Well, the first important thing to note is that there isn't just one hyperreal field, but actually a collection of them. Let me explain.
As you're probably already aware, the real numbers contains all of the integers (or whole numbers). In fact, we can generate all of the positive ones by repeatedly adding one over and over again, like so: \(1, 1+1, 1+1+1, 1+1+1+1,\dots\). This sequence of increasing integers has a very important property: if we take any real number, say \(r\), there is a positive integer \(n\) such that \(r < n\). In other words, there are no real numbers bigger than all of the integers.
If we then reciprocate both numbers (i.e. turn \(r\) into \(\frac{1}{r}\)), we then get that for any positive real number \(r\), there is a positive integer \(n\) such that \(\frac{1}{n} < \frac{1}{r}\). Or, if we set \(\epsilon = \frac{1}{r}\), we get for any positive \(\epsilon\), there's a positive integer \(n\) with \(\frac{1}{n} < \epsilon\). This property is precisely why proof 1 even works: it tells us that the sequence \(\frac{1}{10^i}\) does indeed tend to \(0\).
Alright, so hypothetically, what would happen if we, say, added another number to the real numbers, say \(\omega\), which was bigger than all of the integers? Well, if we do that, we would approach something known as a hyperreal field.
More formally, a hyperreal field is an extension of the real numbers such that there exists elements bigger than every integer. This number system must also preserve first-order logical sentences i.e. a sentence about the real numbers also applies to the hyperreal field, and vice versa. Don't worry about this latter part, it isn't going to be relevant.
What's important to note is that a hyperreal field is still an ordered field, so we can still do addition, multiplication, even division (by non-zero elements). In particular, if \(\omega\) is bigger than all of the integers, then so is \(\omega + 1\), \(\omega - 1\), and \(2 \cdot \omega\). In particular, since all of these numbers are different from each other, this means that there isn't just one 'infinite' number, but a whole lot of them. So, we'll say that a number is 'infinite' if it is bigger than all integers.
Furthermore, since we can still perform division, we can divide \(1\) by \(\omega\). We would get \(\frac{1}{\omega}\), which we'll call \(\alpha\). Now, since for any positive real number \(r\), we had \(\frac{1}{r} < \omega\), we get by reciprocation that \(\alpha = \frac{1}{\omega} < r\), thus we now get that \(\alpha\) is smaller than every positive real numbers. We call \(\alpha\) an 'infinitesimal'. Once again, there isn't just one infinitesimal, but a collection of them.
These 'infinites' and 'infinitesimals' will naturally cause some really interesting behaviours to occur, as we'll soon find out. However, you might first be wondering if such a number system even exists. The quickest way to prove this is to apply Löwenheim-Skolem to the theory of the real numbers. Or, if you'd rather build something more concrete, there is a construction of a hyperreal field using ultrafilters that you can find here.
Alright, so back to the question
So, does \(0.999\dots = 1\) in a hyperreal field? When I first encountered this question, my first instinct was to check if the proofs for \(0.999\dots = 1\) in the real numbers also work in the hyperreals.
First, let's look at the epsilon proof. In order to show \(0.999\dots = 1\), we need to show that for all positive hyperreal \(\epsilon\), there exists a positive integer \(N\) such that for all \(i > N\), \(\frac{1}{10^i} < \epsilon\). However, since we're working in the hyperreals, if \(\epsilon\) is an infinitesimal, this causes \(\frac{1}{10^i} > \epsilon\) for all integers \(i\), so \(0.999\dots\) does not converge to \(1\) in the sense of the epsilon limit definition.
Cool! So in the hyperreal numbers, \(0.999\dots \neq 1\). But just to be sure, let's just check what goes wrong in the second proof that uses algebra. As I've mentioned before, the proof is entirely reliant on the algebra of limits, meaning that as long as this property exists, the proof should be valid. Thank goodness that hyperreal fields are fields, and therefore the algebra of limits is... true. In other words, proof 2 is valid? So \(0.999\dots = 1\)?
Wait, what went wrong?

Changing our Perspective
As it turns out, we made a very bad assumption. At the start of this article, I referred to the epsilon definition of a limit. This is the standard way limits gets defined in the real numbers. Foolishly, I decided to define the number \(0.999\dots\) as the epsilon limit of the sequence \(0.9, 0.09, 0.009, \dots\), without checking to see if this sequence even converges. In fact, the contradiction that we've just uncovered has shown us that the limit doesn't actually exist. More directly, if \(0.999\dots = L\) for some hyperreal \(L\) (in the epsilon limit sense), and \(\epsilon\) is an infinitesimal, then \(L - \epsilon\) is a number that lies between \(L\) and the numbers \(0.9, 0.99, 0.999, \dots\), which contradicts the epsilon definition of limits.
What this entire exercise shows is that the epsilon limit definition sucks when studying hyperreal numbers. So, how do we reconcile this?
Well, this might be slightly underwhelming, but when a mathematician doesn't like a definition, they discard it. Instead, what we can do instead is 'remove' the infinitesimal component of a hyperreal number, and perform the limit there instead. For any finite hyperreal number (a hyperreal number \(h\) is finite if there is a real number \(r\) such that \(|h| < |r|\)) we define \(st(h)\) to be the unique real number \(r\) such that \(r-h\) is \(0\) or an infinitesimal (existence makes use of the completeness axiom of the real numbers). Then, we say that a hyperreal sequence \(a_n\) tends to the real number \(r\) if \(st(a_n)\) tends to \(r\) in the reals.
Using this new definition, we can now define what \(0.999\dots\) means, and unsurprisingly, it equals \(1\).
So, after all this, we have come back full circle to using the same definition as in the reals.
So what's the point in any of this?
Perhaps one might wonder what the use of hyperreal fields are. Perhaps the main use case is in something known as non-standard analysis.
If you've done any amount of calculus, you've probably learned how some things like integration work on an intuitive level. Namely, you might have been taught that you can estimate the area under a curve using rectangles, and as you use thinner and thinner rectangles, the estimate of the area gets better and better. You might also have been taught that integration is about using rectangles with 'infinitesimally' small width. However, as soon as you hit certain milestones in your mathematical journey, you are eventually told that 'infinitesimals' don't exist, and to forget the concept altogether when further studying calculus.
Basically every university and high school teach what is known as standard analysis. This is the study of the real numbers, as well as things like differentiation and integration. This is where one usually encounters things like the epsilon limit, the archimedean property and others. In all of these courses, an emphasis is placed on the non-existence of infinitesimals, instead favouring approaches using limits. We could, however, ask ourselves what would change if the real numbers did in fact have infinitesimals, and this new approach to analysis is what created the field of non-standard analysis.
For instance, in standard analysis, we define differentiation of a function \(f\) at point \(a\) to be the limit \[\lim_{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\] if such a limit exists. The reason for this is because the formula for the slop from \((a, f(a))\) to \(a+h,f(a+h)\) is in fact \(\frac{f(a+h)-f(a)}{h}\). As \(h\) gets smaller, this slope gets closer and closer to being the slope of \(f\) at \(a\). It would be nice if we could just set \(h\) to \(0\) and read off the value of the slope, but unfortunately setting \(h = 0\) leads to divide-by-zero problems, which is why the limit approach gets used.
If however, we had access to infinitesimals, we can instead set \(h\) to be an infinitesimal. This would allow us to approximate the slope of \(f\) at \(a\) more precisely that if \(h\) were any non-zero real number, and since \(h \neq 0\), we would have no divide-by-zero problems.
More precisely, we can define \(df(x,dx) = st\left(\frac{f(x+dx)-f(x)}{dx}\right)\).We can say that \(f\) is differentiable at \(x\) if \(df(x,dx)\) is constant over any choice of \(dx\). The constant criteria is used, because if you zoom into a differentiable function, it will look more and more like a straight line, and so if we move infinitely close to \(f\), the graph should be completely straight, and hence the formula for the slop of a straight line should describe it exactly. This is definitely an interesting approach to calculus.
Whether non-standard analysis is better or worse than standard calculus is hard to say. There are certainly downsides to the non-standard approach (for one thing, to use hyperreal numbers you must convert your function into one that can handle hyperreal number inputs). But this is another topic and I've already inserted enough errors into this article for one day.
