Impossible! An Introduction to Invariants

Over the course of many years, I have been exposed to a variety of mathematical techniques that I've used to solve many a maths problem. And, of them all, there is one technique that I love the most: the invariant. This concept is one that is generally easy to understand, and yet allows us to reason through complex change and transformations. My goal with this article is to expose you to the notion of invariants and convince you of their power, by ultimately solving one of the 1800s greatest puzzles: the 14-15 puzzle.

So, what is an Invariant?

There are many mathematical problems that deals with change. Take, for instance, a Rubik's Cube. The toy is pretty easy to play with; to move the pieces around, simply twists the sides. And yet, anyone who's held a Rubik's Cube knows that even just a couple of twists is enough to make an inexperienced person unable to move the pieces back in place. Its complexity is part of why the Rubik's Cube is still popular today.

We could ask ourselves simple questions about the cube. For instance, which colour configuration is it possible to achieve? This is certainly not an easy question to answer, and any attempt to catalogue them through brute force is hard. So, rather than observing the changes caused by each move, we could instead observe that which doesn't change. For instance, look at the centres of the cube when you twist a side: while certainly the centre pieces might rotate, they don't actually move off of their position. This simple observation tells us something very important: namely, that the yellow centre piece will always be opposite to the white centre piece, and so on. Simply by noticing what doesn't change, we found a large number of colour configurations that isn't possible.

What we have discovered is an invariant. An invariant is, simply put, a property or quantity of our object that, no matter what we do to it, never changes. In the case of the Rubik's Cube, the position of the centre pieces is an invariant (with respect to the allowed moves. Obviously, if you broke the cube into pieces and built it back together, you can put the centre pieces wherever you please). And, while the study of the Rubik's Cube is certainly interesting (and maybe the subject of a future article), it's probably best to first look at some simpler examples.

Problem 1 - Fair Distribution

Let's say we have \(100\) piles of pebbles. \(33\) of the piles contains \(3\) pebbles, \(33\) of the piles contains \(4\) pebbles, and the remaining \(34\) piles contains \(5\) pebbles. The only move we are allowed to do is merge two existing pile into one, and the task is to merge piles of pebbles together until we end up with two or more piles, each containing the same number of pebbles.

We could certainly try a few merges to see what happens, however it would be very tedious to try every possibility and see what we get. Let's instead try and find an invariant. Well, one thing that definitely doesn't change is the total number of pebbles: we always have \(33 \cdot 3 + 33 \cdot 4 + 34 \cdot 5 = 401\) pebbles. By the way, if you were thinking that these numbers were deliberately picked, you are right: \(401\) is a prime number. This means that it is not actually possible to divide the \(401\) pebbles into at least two piles containing the same number of pebbles. The given task is impossible.

Alright? Let's go a little deeper.

Problem 2 - Chessboard and Dominoes

This was one of the earlier problems that I encountered when I first learned of invariants, and it stuck with me because of how elegant the solution was. In fact, I like this problem so much that I feel a little bad spoiling the solution (by which I mean I strongly encourage you give a go solving this problem before reading on).

We have a standard \(8 \times 8\) chessboard, except we have removed two opposite corners. We also have \(31\) dominoes that can perfectly cover two adjacent squares on the chessboard. The problem is as follows: is it possible to fully cover the chessboard with dominoes, such that no two dominoes overlap or hang off the edge of the board?

Once again, while we could try every possibility, there is a better way to solve this problem that stems from a simple observation. Because of how a chessboard is coloured, everytime you lay down a domino, it covers exactly one white square and one black square. What this means is that the difference between the number of visible black and white squares stays constant i.e. If \(B\) is the number of black uncovered squares, and \(W\) is the number of white uncovered squares, then \(W-B\) doesn't change when we put down a domino.

This observation is very useful. Suppose the two removed corners are black. Then, at the start, there are \(32\) white squares and \(30\) black squares, thus \(W-B = 2\). However, if the dominoes were to cover the entire chessboard, then we would have \(0\) uncovered white squares and \(0\) uncovered black squares, so \(W-B=0\). Since the value of \(W-B\) doesn't change whenever we put down a domino, this leads to an imposibility. We have therefore shown that it is not possible to cover the chessboard with non-overlapping dominoes.

A quick interlude

Hopefully these first two examples have been illustrative as to the power of invariants. Instead of having to make complicated analysis and calculations, we just needed to observe some property that cannot change based on the rules, and then show that any solution must break this property. I wanted to cover one more famous problem, however to do so, I need to first explain the next invariant, as it is a little bit more complicated.

Suppose we have some number of balls (in this case, \(6\)), each sitting on their own pedestal, and both the balls and pedestals are numbered.

A permutation is any rearrangement of the balls on the pedestal.

One way to construct a permutation from our initial position of balls is by repeatedly swapping two balls. We first swap the ball we want into the first position, and then do the same with the ball we want in the second position etc.

One question we could therefore ask ourselves is how many swaps would we need to get some permutation. For instance, it takes \(4\) swaps to go from \([1,2,3,4,5,6]\) to \([3,4,6,1,5,2]\).

Note that while this is the number of swaps necessary for the most efficient solution, we could certainly do it using \(6\), \(8\), \(20\) or even \(100\) swaps. However, we interestingly cannot do it in \(5\) swaps, or \(7\), or in fact any odd number of swaps (feel free to try). Something similar happens with \([3,4,6,1,2,5]\), namely that we can do it using \(5\), \(7\), or \(101\) swaps, but not with \(6\), \(8\) or any even number of swaps. This phenomenon is known as permutation parity, namely that from an initial position, it might take an even number of swaps to reach a certain permutation, or an odd number of swaps, but never both at the same time. The technical details can be found here.

Alright, let's look at the final problem.

Problem 3 - the 14-15 puzzle

The subject of this problem is a tile-sliding puzzle. The puzzle is often made from wood or plastic, and has 15 square pieces that slides around in the casing. Some of these puzzles have a picture on them, and your goal is to move the tiles around so that they're in the right place to reveal the picture.

For this problem though, the tiles have the numbers \(1\) to \(15\) on them, and the goal, after mixing the tiles up, is to rearrange the pieces such that all of the numbers are in order when reading them from left to right. This was a toy that I often played with, to the point of being able to solve them consistently in under a minute. Though, One thing that struck me as quite interesting is that once I got the first 12 tiles in the right place, the last three tiles (namely the \(11\),\(12\) and \(15\) tiles) always fell quite quickly into place. I never ended up in the situation where, for instance, the \(11\) and \(12\) tile were swapped around. As it turns out, this observation is related to a 'competition' set by Sam Loyd in the late 1800s.

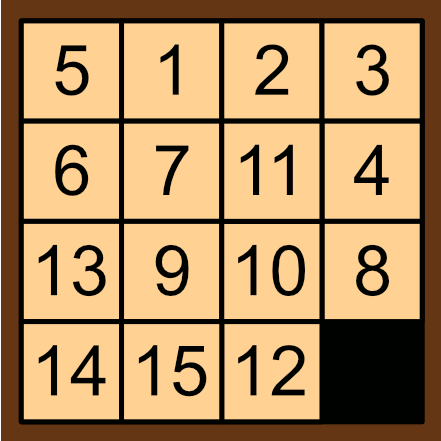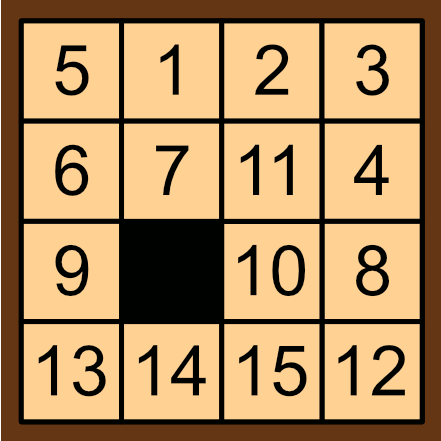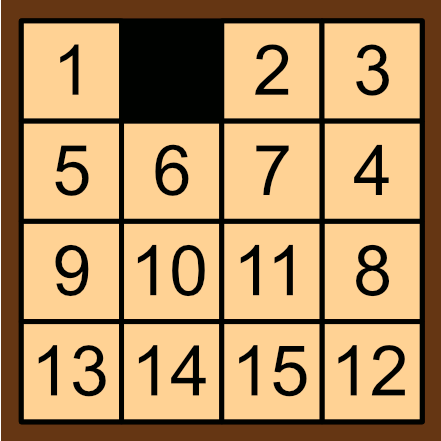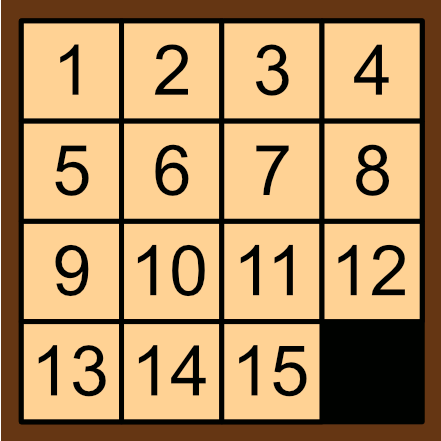
This puzzle was originally invented by Noyes Chapman in the 1870s, and it was so successful it began a craze in 1880. A few years later, Sam Loyd sold a similar puzzle, except with the \(14\) and \(15\) tiles swapped around. He challenged people to solve this version of the puzzle, and even offered $1000 for any correct solutions (he also claimed to have invented this puzzle). As the story goes, many people claimed to have solved it, but the money was never awarded. This is because, as proven by Johnson and Story in 1879, this puzzle is unsolvable.

To understand why, lets consider this puzzle in the context of permutation parity. We can imagine the tiles being equivalent to the balls from the previous section, the difference being that the pedestals are arranged into a square instead of a line (and the \(14\) and \(15\) pedestal are swapped around). We can also imagine a phantom tile \(16\) that takes the place of the empty square in the puzzle. The puzzle can therefore be reframed as follows: if we are only allowed to swap the \(16\) tile with one of its neigbour, can we find a series of swaps that gets us from our initial position with the \(14\) and \(15\) tiles swapped, to the 'solved' position with all of the pieces in the right place.

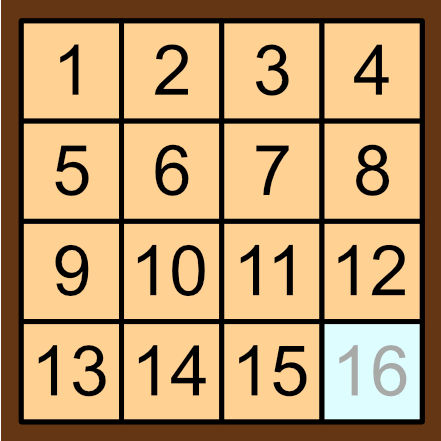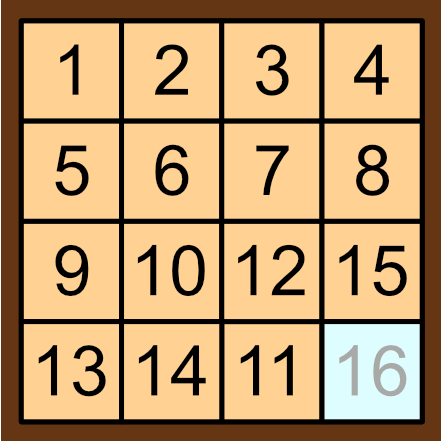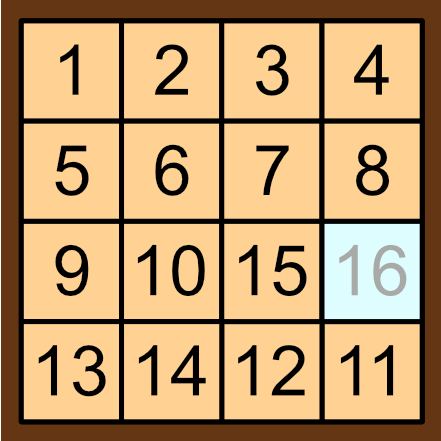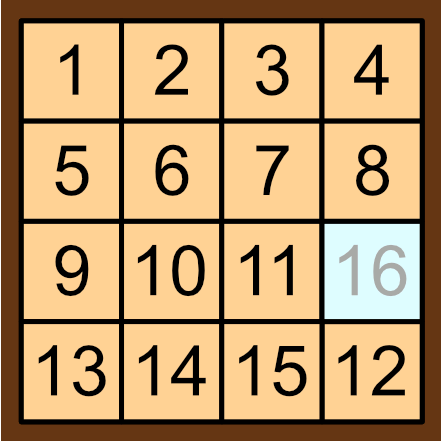
As I've strongly hinted, the solution will involve permutation parity. Firstly, we notice that, if a solution to this puzzle exists, then we have performed an even number of neighbour swaps with the 16 tile. This is because, if we perform an odd number of swaps, then the \(16\) tile won't be in the bottom right. One way to see this is by colouring the tile grid like a chessboard, with the \(16\) tile's square being white. Every swap causes the \(16\) tile to move to a different coloured square, and in particular the \(16\) tile will be on a white square after an even number of swaps, and on a black square after an odd number of swaps. Therefore, if the \(16\) tile is to end up back in the bottom right white tile, it must happen after an even number of swaps.

However, let's consider what we've just shown. We have just performed an even number of swaps, in order to swap the \(14\) and \(15\) tile. The issue is that, if we replace the tiles with the balls and pedestals from the previous section (thus allowing us to make any swap), then our solution to the 14-15 puzzle gives us a procedure to swap the \(14\) and \(15\) ball using an even number of swaps, or in other words, the 'solved' position can be reached from the initial position using both an odd and even number of swaps, which contradicts our property of permutation parity. This contradiction arises if we assume a solution to the 14-15 puzzle exists, therefore a solution cannot exist.

Final Thoughts

If you've made it here, congratulations! You now have a more thorough understanding of invariants through these easy (and less easy) examples. In all of these problems, we have used invariants to show that a solution doesn't exist, but that's not its only use: if a solution does exists, we can use an invariant to predict what it might look like (but this is the subject of another day). In any case, thank you for reading this article. I hope the explanations were clear, since this is after all the first proper article I've written for this site. If you want to contact me, my socials are ...somewhere.

In any case, if this stuff interests you, I strongly encourage you to seek out more problems like this, and I'll leave you with a problem that can be solved using what you've learned so far:

You and nine of your friends (so \(10\) people in total) have just found a crazy machine. If one person in your friend group inserts a coin into the machine, it will give a coin to every other person in the friend group. At the start, only you have one coin; everybody else have none. Is there a way to use the machine so that everybody has the same number of coins?